|
Có 120 bài học trong chuyên mục Bài học trực tuyến được phân loại theo đối tượng THPT
 Giới thiệu nhanh phần mềm Luyện thi đại học môn Sinh vật (Ngày gửi bài: 12/06/2012 - Thảo luận: 0 - Số lượt đọc: 11482) Giới thiệu nhanh phần mềm Luyện thi đại học môn Sinh vật (Ngày gửi bài: 12/06/2012 - Thảo luận: 0 - Số lượt đọc: 11482)
 Bùi Việt Hà, Công ty Công nghệ Tin học Nhà trường Bùi Việt Hà, Công ty Công nghệ Tin học Nhà trường
Chúng tôi xin giới thiệu với các bạn học sinh đang chuẩn bị bước vào kỳ thi tuyển sinh sắp tới và các bậc cha mẹ học sinh các phần mềm rất đặc biệt của Công ty Công nghệ Tin học Nhà trường. Đó là 4 phần mềm Luyện thi đại học, cao đẳng các môn Tiếng Anh, Vật lý, Hóa học và Sinh học.
Xem tiếp  |
 Giới thiệu nhanh phần mềm Luyện thi đại học môn Hóa học (Ngày gửi bài: 12/06/2012 - Thảo luận: 0 - Số lượt đọc: 10770) Giới thiệu nhanh phần mềm Luyện thi đại học môn Hóa học (Ngày gửi bài: 12/06/2012 - Thảo luận: 0 - Số lượt đọc: 10770)
 Bùi Việt Hà, Công ty Công nghệ Tin học Nhà trường Bùi Việt Hà, Công ty Công nghệ Tin học Nhà trường
Trong các môn thi tuyển sinh Đại học, Cao đẳng có 4 môn được Bộ GD&ĐT qui định là kiểm tra trắc nghiệm hoàn toàn, đó là các môn Tiếng Anh, Vật lý, Hóa học và Sinh học.
Chúng tôi xin giới thiệu với các bạn học sinh đang chuẩn bị bước vào kỳ thi tuyển sinh sắp tới và các bậc cha mẹ học sinh các phần mềm rất đặc biệt của Công ty Công nghệ Tin học Nhà trường. Đó là 4 phần mềm Luyện thi đại học, cao đẳng các môn Tiếng Anh, Vật lý, Hóa học và Sinh học.
Xem tiếp  |
 Giới thiệu gói phần mềm S11 dành cho các học sinh chuẩn bị vào Lớp 11, món quà đặc biệt vui hè 2012 cho mọi gia đình (Ngày gửi bài: 11/06/2012 - Thảo luận: 0 - Số lượt đọc: 7223) Giới thiệu gói phần mềm S11 dành cho các học sinh chuẩn bị vào Lớp 11, món quà đặc biệt vui hè 2012 cho mọi gia đình (Ngày gửi bài: 11/06/2012 - Thảo luận: 0 - Số lượt đọc: 7223)
 Chương trình khuyến mại HÈ 2012 của công ty School@net có gì đặc biệt? Có gói quà nào dành cho các em học sinh lứa tuổi THPT hay không? Chương trình khuyến mại HÈ 2012 của công ty School@net có gì đặc biệt? Có gói quà nào dành cho các em học sinh lứa tuổi THPT hay không?
Chúng tôi xin giới thiệu với các bậc phụ huynh các gói quà đặc biệt này trong dịp hè 2012. Chương trình khuyến mại đặc biệt này chỉ có thời hạn từ nay đến 30/6/2012.
Công ty Công nghệ Tin học Nhà trường xin giới thiệu với các gia đình có con là học sinh sắp bước vào lớp 11 gói phần mềm đặc biệt S11 dành riêng cho lứa tuổi này.
Xem tiếp  |
 Toán 12 - Chương III - Bài 5. Ôn tập cuối năm (Ngày gửi bài: 21/11/2011 - Thảo luận: 0 - Số lượt đọc: 13882) Toán 12 - Chương III - Bài 5. Ôn tập cuối năm (Ngày gửi bài: 21/11/2011 - Thảo luận: 0 - Số lượt đọc: 13882)
I - Bài tập tự luận 1. Cho hình lăng trụ ABC.A’B’C’ với cạnh bên không vuông góc với mặt đáy. Gọi 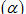 là mặt phẳng vuông góc với các cạnh bên của hình lăng trụ và của chúng tại P, Q, R. Phép tịnh tiến theo vectơ là mặt phẳng vuông góc với các cạnh bên của hình lăng trụ và của chúng tại P, Q, R. Phép tịnh tiến theo vectơ  biến tam giác PQR thành tam giác P’Q’R’. biến tam giác PQR thành tam giác P’Q’R’. Xem tiếp  |
 Toán 12 - Chương II - Bài 2. Khái niệm về mặt tròn xoay (Ngày gửi bài: 15/11/2011 - Thảo luận: 0 - Số lượt đọc: 12855) Toán 12 - Chương II - Bài 2. Khái niệm về mặt tròn xoay (Ngày gửi bài: 15/11/2011 - Thảo luận: 0 - Số lượt đọc: 12855)
Mặt cầu là một trường hợp đơn giản của các mặt tròn xoay mà ta sẽ nói đến trong mục này. Trước hết, ta định nghĩa trục của đường tròn : Trục của đường tròn (O ; R) là đường thẳng đi qua O và vuông góc với mặt phẳng chưa đường tròn đó. Dễ thấy rằng khi điểm M không nằm trên đường thẳng  thì có một đường tròn duy nhất đi qua M và có trục là thì có một đường tròn duy nhất đi qua M và có trục là  , kí hiệu đường tròn đó là , kí hiệu đường tròn đó là 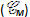 (h.37). (h.37). Xem tiếp  |
 Toán 12- Nâng Cao - Chương II - Bài 1. MẶT CẦU, KHỐI CẦU (Ngày gửi bài: 15/11/2011 - Thảo luận: 0 - Số lượt đọc: 20232) Toán 12- Nâng Cao - Chương II - Bài 1. MẶT CẦU, KHỐI CẦU (Ngày gửi bài: 15/11/2011 - Thảo luận: 0 - Số lượt đọc: 20232)
CHƯƠNG II. MẶT CẦU, MẶT TRỤ, MẶT NÓN Trong đời sống hằng ngày, chúng ta thường gặp những đồ vật có dạng hình cầu, hình trụ hoặc hình nón. Học xong chương này, học sinh cần hình dung được thế nào là mặt cầu, mặt trụ, mặt nón và những hình có quan hệ đến những mặt đó. Học sinh cần nhớ các công thức về diện tích và thể tích của hình cầu, hình trụ và hình nón.Xem tiếp  |
 Toán 12- Nâng Cao - Chương I - Bài 5. ÔN TẬP CHƯƠNG I (Ngày gửi bài: 15/11/2011 - Thảo luận: 0 - Số lượt đọc: 11332) Toán 12- Nâng Cao - Chương I - Bài 5. ÔN TẬP CHƯƠNG I (Ngày gửi bài: 15/11/2011 - Thảo luận: 0 - Số lượt đọc: 11332)
ÔN TẬP CHƯƠNG I I - Kiến thức cần nhớ 1. Hình đa diện gồm một số hữu hạn đa giác phẳng thỏa mãn hai điều kiện : a) Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung. b) Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác. Xem tiếp  |
 Toán 12- Nâng Cao - Chương I - Bài 4 THỂ TÍCH CỦA KHỐI ĐA DIỆN (Ngày gửi bài: 12/11/2011 - Thảo luận: 0 - Số lượt đọc: 17475) Toán 12- Nâng Cao - Chương I - Bài 4 THỂ TÍCH CỦA KHỐI ĐA DIỆN (Ngày gửi bài: 12/11/2011 - Thảo luận: 0 - Số lượt đọc: 17475)
§4 THỂ TÍCH CỦA KHỐI ĐA DIỆN 1. Thế nào là thể tích của một khối đa diện ? Chúng ta biết rằng trong mặt phẳng, mỗi đa giác có một diện tích. Đó là số đo phần mặt phẳng mà đa giác đó chiếm chỗ. Tương tự như vậy, các khối đa diện chiếm những phần không gian lớn nhỏ khác nhau. Thể tích của mỗi khối đa diện là số đo của phần không gian mà nó chiếm chỗ.Xem tiếp  |
 Toán 12- Nâng Cao - Chương I - Bài 2. PHÉP ĐỐI XỨNG QUA MẶT PHẲNG (Ngày gửi bài: 11/11/2011 - Thảo luận: 0 - Số lượt đọc: 29666) Toán 12- Nâng Cao - Chương I - Bài 2. PHÉP ĐỐI XỨNG QUA MẶT PHẲNG (Ngày gửi bài: 11/11/2011 - Thảo luận: 0 - Số lượt đọc: 29666)
§2 PHÉP ĐỐI XỨNG QUA MẶT PHẲNG
VÀ SỰ BẰNG NHAU CỦA CÁC KHỐI ĐA DIỆN
Phép biến hình trong không gian được định nghĩa tương tự như trong mặt phẳng : Phép biến hình F trong không gian là một quy tắc để với mỗi điểm M (trong không gian), xác định được một điểm M’ duy nhất gọi là ảnh của điểm M qua phép biến hình F. Ta còn nói F biến điểm M thành điểm M’ và kí hiệu M’ = F(M).
Xem tiếp  |
 Toán 11- Nâng Cao - Bài Tập Ôn Cuối Năm (Ngày gửi bài: 10/11/2011 - Thảo luận: 0 - Số lượt đọc: 9766) Toán 11- Nâng Cao - Bài Tập Ôn Cuối Năm (Ngày gửi bài: 10/11/2011 - Thảo luận: 0 - Số lượt đọc: 9766)
Bài Tập Ôn Cuối Năm 1. Cho tam giác ABC và các điểm M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. a) Xét bốn tam giác APN, PBM, NMC, MNP. Tìm phép dời hình biến tam giác APN lần lượt thành một trong ba tam giác còn lại.Xem tiếp  |
 Toán 11 - Chương III - Bài 6. Ôn tập chương III (Ngày gửi bài: 10/11/2011 - Thảo luận: 0 - Số lượt đọc: 12177) Toán 11 - Chương III - Bài 6. Ôn tập chương III (Ngày gửi bài: 10/11/2011 - Thảo luận: 0 - Số lượt đọc: 12177)
I - Tóm tắt những kiến thức cần nhớ 1. Định nghĩa vectơ và các phép toán vectơ trong không gian cũng giống như trong mặt phẳng. Ngoài ra: a) Ba vectơ gọi là đồng phẳng khi các giá của chúng cùng song song với một mặt phẳng. b) Điều kiện cần và đủ để ba vectơ 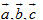 đồng phẳng là có ba số m, n, p không đồng thời bằng 0 sao cho đồng phẳng là có ba số m, n, p không đồng thời bằng 0 sao cho  . . Xem tiếp  |
 Toán 11- Nâng Cao - Chương III - Bài 5. Khoảng cách (Ngày gửi bài: 09/11/2011 - Thảo luận: 0 - Số lượt đọc: 14115) Toán 11- Nâng Cao - Chương III - Bài 5. Khoảng cách (Ngày gửi bài: 09/11/2011 - Thảo luận: 0 - Số lượt đọc: 14115)
Bài 5. Khoảng cách 1. Khoảng cách từ một điểm đến một mặt phẳng, đến một đường thẳng Để đi đến khái niệm khoảng cách từ một điểm đến một mặt phẳng hoặc một đường thẳng, ta xét hình chiếu vuông góc của điểm đó trên mặt phẳng hoặc đường thẳng. Xem tiếp  |
 Toán 11 - Chương III. Bài 3. Đường thẳng vuông góc với mặt phẳng (Ngày gửi bài: 08/11/2011 - Thảo luận: 0 - Số lượt đọc: 15702) Toán 11 - Chương III. Bài 3. Đường thẳng vuông góc với mặt phẳng (Ngày gửi bài: 08/11/2011 - Thảo luận: 0 - Số lượt đọc: 15702)
1. Định nghĩa đường thẳng vuông góc với mặt phẳng Bài toán 1 Cho hai đường thẳng cắt nhau b và c cùng nằm trong mặt phẳng (P). Chứng minh rằng nếu đường thẳng a vuông góc với cả b và c thì nó vuông góc với mọi đường thẳng nằm trong (P). Xem tiếp  |
 Toán 11- Nâng Cao - Chương III - Bài 2. Hai đường thẳng vuông góc (Ngày gửi bài: 08/11/2011 - Thảo luận: 0 - Số lượt đọc: 10329) Toán 11- Nâng Cao - Chương III - Bài 2. Hai đường thẳng vuông góc (Ngày gửi bài: 08/11/2011 - Thảo luận: 0 - Số lượt đọc: 10329)
Bài 2. Hai đường thẳng vuông góc 1. Góc giữa hai đường thẳng Cho hai đường thẳng ∆1, ∆2 bất kì trong không gian. Từ điểm O nào đó, ta vẽ hai đường thẳng ∆’1, ∆’2 lần lượt song song (hoặc trùng) với ∆1, ∆2. Dễ thấy rằng khi điểm O thay đổi thì góc giữa ∆’1 và ∆’2 không thay đổi (h.93).Xem tiếp  |
 Toán 11 - Chương III. Bài 1. Vectơ trong không gian. Sự đồng phẳng của các vectơ (Ngày gửi bài: 07/11/2011 - Thảo luận: 0 - Số lượt đọc: 15379) Toán 11 - Chương III. Bài 1. Vectơ trong không gian. Sự đồng phẳng của các vectơ (Ngày gửi bài: 07/11/2011 - Thảo luận: 0 - Số lượt đọc: 15379)
Ở chương II, chúng ta đã xét quan hệ song song trong không gian. Trong chương này ta nghiên cứu quan hệ vuông góc giữa hai đường thẳng, giữa đường thẳng với mặt phẳng, giữa hai mặt phẳng. Kiến thức về vectơ là cơ sở để xây dựng quan hệ vuông góc trong không gian. Khi học chương này, học sinh cần biết vận dụng các kiến thức đã có về vectơ trong mặt phẳng để áp dụng vào không gian, đồng thời bước đầu giải quyết được một số bài toán hình học không gian có liên quan đến các yếu tố vuông góc. Xem tiếp  |
 Toán 11 - Chương II - Bài 6. Ôn tập chương II (Ngày gửi bài: 07/11/2011 - Thảo luận: 0 - Số lượt đọc: 11024) Toán 11 - Chương II - Bài 6. Ôn tập chương II (Ngày gửi bài: 07/11/2011 - Thảo luận: 0 - Số lượt đọc: 11024)
I - Tóm tắt những kiến thức cần nhớ 1. Một mặt phẳng được xác định nếu biết một trong các điều kiện sau đây: a) Mặt phẳng đó đi qua ba điểm không thẳng hàng. b) Mặt phẳng đó đi qua một điểm và một đường thẳng không chứa điểm ấy. c) Mặt phẳng đó đi qua hai đường thẳng cắt nhau. Xem tiếp  |
 Toán 11 - Chương II - Bài 5. Phép chiếu song song (Ngày gửi bài: 05/11/2011 - Thảo luận: 0 - Số lượt đọc: 6843) Toán 11 - Chương II - Bài 5. Phép chiếu song song (Ngày gửi bài: 05/11/2011 - Thảo luận: 0 - Số lượt đọc: 6843)
1. Định nghĩa phép chiếu song song Trong không gian cho mặt phẳng (P) và đường thẳng l cắt mp(P). Với mỗi điểm M trong không gian, vẽ đường thẳng đi qua M và song song hoặc trùng với l. Đường thẳng này cắt mp(P) tại một điểm M’ nào đó (h.73). Xem tiếp  |
 Toán 11 - Chương I - Bài 7. Phép đồng dạng (Ngày gửi bài: 02/11/2011 - Thảo luận: 0 - Số lượt đọc: 7890) Toán 11 - Chương I - Bài 7. Phép đồng dạng (Ngày gửi bài: 02/11/2011 - Thảo luận: 0 - Số lượt đọc: 7890)
1. Định nghĩa phép đồng dạng  1 Phép dời hình và phép vị tự có phải là những phép đồng dạng hay không? 1 Phép dời hình và phép vị tự có phải là những phép đồng dạng hay không?
Nếu có thì tỉ số đồng dạng là bao nhiêu? Xem tiếp  |
 Toán 11 - Chương I - Bài 6. Phép vị tự (Ngày gửi bài: 01/11/2011 - Thảo luận: 0 - Số lượt đọc: 21185) Toán 11 - Chương I - Bài 6. Phép vị tự (Ngày gửi bài: 01/11/2011 - Thảo luận: 0 - Số lượt đọc: 21185)
Chúng ta hãy quan sát hai bức chân dung ở hình vẽ dưới đây. Tuy kích thước của chúng khác nhau nhưng hình dạng của chúng rất “giống nhau” (ta nói chúng “đồng dạng” với nhau). Vì bức nhỏ hơn là chân dung của nhà toán học Hin-be nên bức lớn hơn cũng là chân dung của nhà toán học đó. Xem tiếp  | Có 120 bài học trong chuyên mục Bài học trực tuyến được phân loại theo đối tượng THPT
|




 Bùi Việt Hà, Công ty Công nghệ Tin học Nhà trường
Bùi Việt Hà, Công ty Công nghệ Tin học Nhà trường
 Bùi Việt Hà, Công ty Công nghệ Tin học Nhà trường
Bùi Việt Hà, Công ty Công nghệ Tin học Nhà trường Chương trình khuyến mại HÈ 2012 của công ty School@net có gì đặc biệt? Có gói quà nào dành cho các em học sinh lứa tuổi THPT hay không?
Chương trình khuyến mại HÈ 2012 của công ty School@net có gì đặc biệt? Có gói quà nào dành cho các em học sinh lứa tuổi THPT hay không? Chương trình khuyến mại HÈ 2012 của công ty School@net có gì đặc biệt? Có gói quà nào dành cho các em học sinh lứa tuổi THPT hay không?
Chương trình khuyến mại HÈ 2012 của công ty School@net có gì đặc biệt? Có gói quà nào dành cho các em học sinh lứa tuổi THPT hay không? Như đã thông báo, hiện công ty Công nghệ Tin học Nhà trường đang thực hiện việc đưa nội dung của SGK môn Toán Hình học của các lớp từ 6 đến 12 chương trình Nâng cao lên Website của công ty.
Như đã thông báo, hiện công ty Công nghệ Tin học Nhà trường đang thực hiện việc đưa nội dung của SGK môn Toán Hình học của các lớp từ 6 đến 12 chương trình Nâng cao lên Website của công ty. 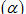 là mặt phẳng vuông góc với các cạnh bên của hình lăng trụ và của chúng tại P, Q, R. Phép tịnh tiến theo vectơ
là mặt phẳng vuông góc với các cạnh bên của hình lăng trụ và của chúng tại P, Q, R. Phép tịnh tiến theo vectơ  biến tam giác PQR thành tam giác P’Q’R’.
biến tam giác PQR thành tam giác P’Q’R’. .
.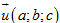 (h.66). Vì
(h.66). Vì  nên ta phải có .
nên ta phải có .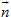 ≠ 0 gọi là vectơ pháp tuyến của mặt phẳng (α) nếu giá của
≠ 0 gọi là vectơ pháp tuyến của mặt phẳng (α) nếu giá của 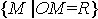 . Khối cầu S(O ; R) là tập hợp
. Khối cầu S(O ; R) là tập hợp  .
. . Xét một đường thẳng l cắt
. Xét một đường thẳng l cắt  thì có một đường tròn duy nhất đi qua M và có trục là
thì có một đường tròn duy nhất đi qua M và có trục là 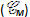 (h.37).
(h.37). gọi là phép vị tự. Điểm O gọi là tâm vị tự, số k gọi là tỉ số vị tự.
gọi là phép vị tự. Điểm O gọi là tâm vị tự, số k gọi là tỉ số vị tự. Như đã thông báo, hiện công ty Công nghệ Tin học Nhà trường đang thực hiện việc đưa nội dung của SGK môn Toán Hình học của các lớp từ 6 đến 12 chương trình Nâng cao lên Website của công ty.
Như đã thông báo, hiện công ty Công nghệ Tin học Nhà trường đang thực hiện việc đưa nội dung của SGK môn Toán Hình học của các lớp từ 6 đến 12 chương trình Nâng cao lên Website của công ty. 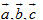 đồng phẳng là có ba số m, n, p không đồng thời bằng 0 sao cho
đồng phẳng là có ba số m, n, p không đồng thời bằng 0 sao cho  .
.



